大気科学演習１

gnuplot

フィッティング

データを任意の関数でフィティングする．

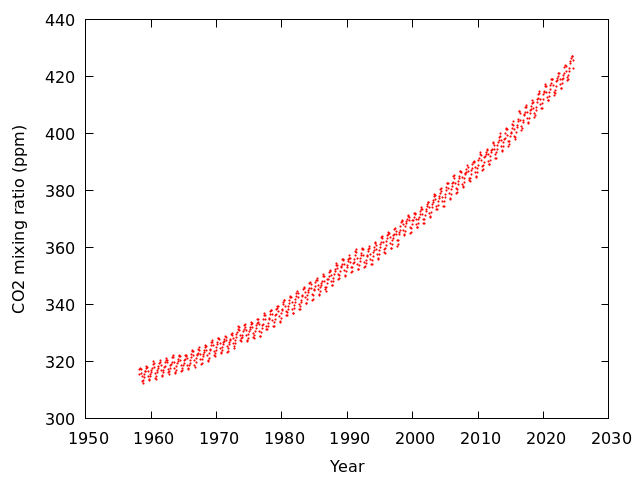
マウナロアで測定されたCO2濃度を図にしてみる

gnuplot> plot '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 with points pointtype 7 pointsize 0.2

データを関数でフィッティングするときは，(1)関数を定義，(2)初期値の設定，(3)フィッティング，の順番でおこなう．(2)は省略することもできるが，初期値がダサいとフィッティングに失敗することがある．

とりあえず，やってみる

gnuplot> f(x)=a+b*(x-1970)
gnuplot> fit f(x) '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 via a,b
gnuplot> plot '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 with points pointtype 7 pointsize 0.2, f(x)

１行目で関数を定義，２行目でフィッティング，３行目は結果の表示，である． フィッティングをすると，なんかいろいろなことが表示される(ちゃんと読んだら，フィッティングして決まったパラメタの値とか，その当てはまり具合とか，そういうことが書いてあるとわかる)． 一次関数でフィッティングしたら，こういう結果になるだろうという結果になっている．

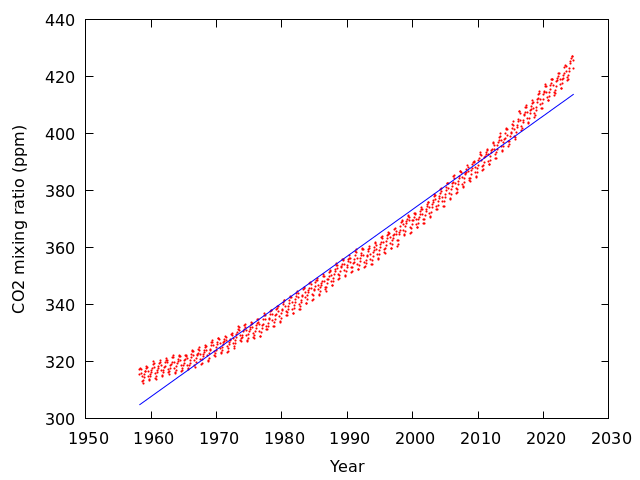
関数を変えて試してみる．

gnuplot> g(x)=a+b*exp((x-1970)/c)
gnuplot> fit g(x) '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 via a,b,c
gnuplot> plot '/home/atmos/ipesc/sample/co2/mlo.txt' using 3.4 with points pointtype 7 pointsize 0.2, g(x)

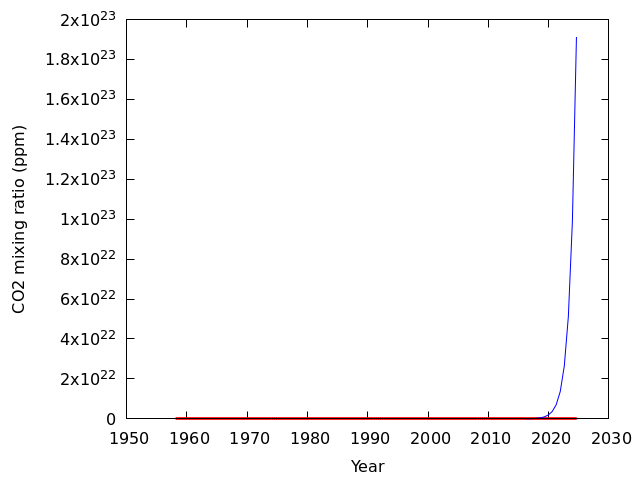
なんか上手くいっているように見えない． 初期値がいまいちだったため(初期値を与えない場合は適当な値が設定される)，最適解を見つけることに失敗したのだと予想される． 初期値を設定してやり直してみる．

gnuplot> a=320
gnuplot> b=40
gnuplot> c=50
gnuplot> fit g(x) '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 via a,b,c
gnuplot> plot '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 with points pointtype 7 pointsize 0.2, g(x)

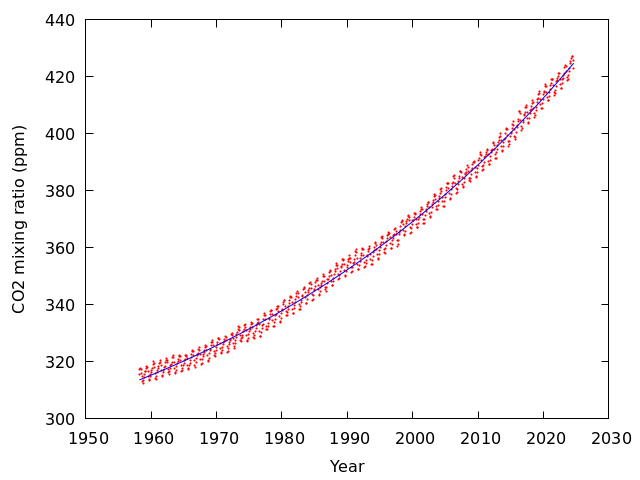
今度はいい感じの結果が得られた． 答えに近い初期値を与えれば，解はちゃんと見つかる． とはいえ，答えがわからない場合も多い(というか，答えを知っていたらフィッティングなどする必要がない)ので，答えに近い初期値を与えればよいというのは理屈では正しくとも役に立たないことが多かったりする．

CO2は季節変化しているので，それもフィッティングしてみる．

gnuplot> h(x)=g(x)+d*sin(2*pi*x/e+f)
gnuplot> fit h(x) '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 via d,e,f
gnuplot> set samples 3000
gnuplot> plot '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 with points pointtype 7 pointsize 0.2, h(x)

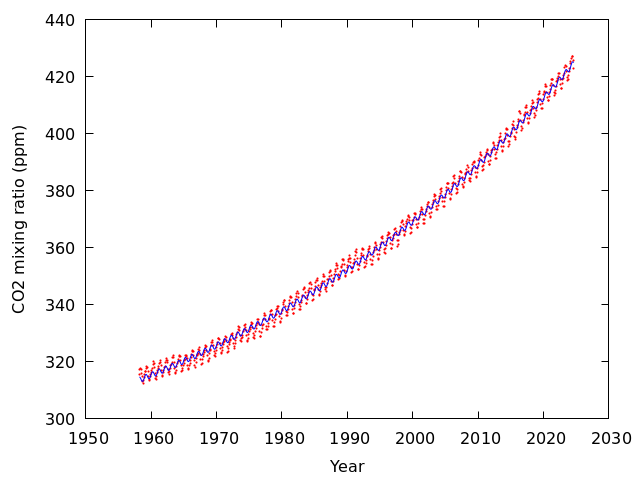
上手くいっていない(季節変化が過小評価されている)． 初期値を設定してやり直す．

gnuplot> d=4
gnuplot> e=1
gnuplot> f=1
gnuplot> fit h(x) '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 via d,e,f
gnuplot> plot '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 with points pointtype 7 pointsize 0.2, h(x)

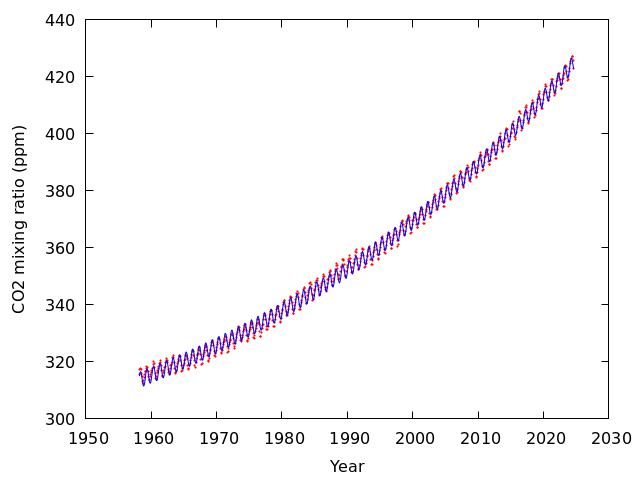
フィッティングの結果はfitを実行するたびに表示されるが，それと同じものが fit.log という名前のファイルに書き込まれている． gnuplotを終了して見てみる．

gnuplot> exit
$ cat fit.log

季節変化の振幅は d の２倍なので 5 (ppm) くらい，周期(e)は 0.999966 (year) となっている． 周期が１年になっていることは，そうであるべきものが正しく求まっているということで，とてもよいことである． 繰り返しになるが，計算機が出した結果を鵜呑みにしてはいけない． 常識やその他の知識に照らし合わせて，おかしなことが起こっていないかどうか，確認できることは確認しなければならない．

補足

何が目的であるのかに依存するが，周期は１年であるとわかっているのであれば，パラメタ e を求める必要はなく，最初から関数を

gnuplot> h(x)=g(x)+d*sin(2*pi*x+f)

で与えて，

gnuplot> fit h(x) '/home/atmos/ipesc/sample/co2/mlo.txt' using 3:4 via a,b,c,d,f

でフィットするのが正解という場合もあるだろう．

蛇足：フィッティングを使って平均の計算

関数 f(x)=a にフィッティングして得られる a の値はデータの平均になるので，以下のようにしてデータの平均を求めることができる．

gnuplot> f(x)=a
gnuplot> fit f(x) 'data.dat' using 0:1 via a

例えば，アメダスのデータから日平均気温の平均を求める場合

gnuplot> f(x)=a
gnuplot> set datafile separator ','
gnuplot> fit f(x) '/home/atmos/ipesc/sample/amedas/Okayama_Okayama_2018.csv' using 0:2 via a

フィッティングの結果は

a = 16.329

なので，2018年の日平均気温の平均は16.329度．